円 速度ベクトル
ホドグラフとは コトバンク
Q5 1 Xy面内で等速円運動 軌道半径はr 角速度の大きさはw Yahoo 知恵袋

円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ

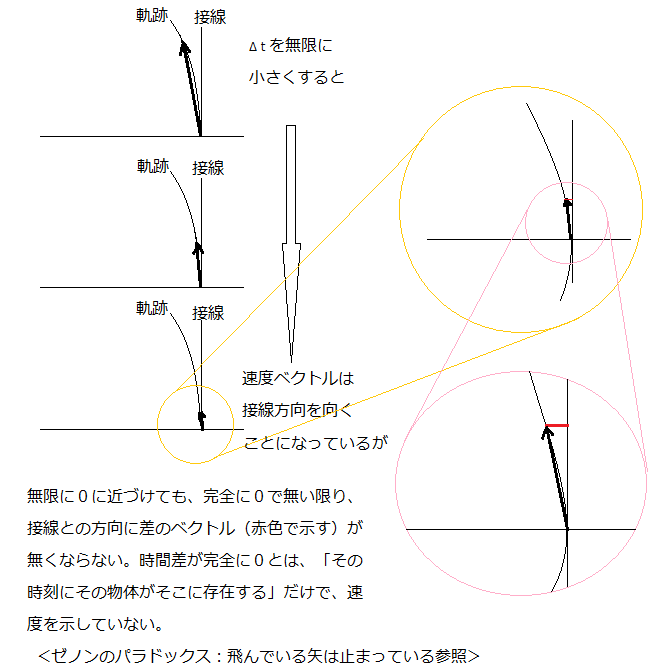
無題ドキュメント

1番の質問です 下の2行の式を用いると Dr Dtが出てくる 物理に関する質問 勉強質問サイト
Q Tbn And9gctr8ebbfhhwhp4b Tj0bcaqo1o6xhtoycc2orj3pzg Usqp Cau
波のベクトル表記:波の振動方向を決める 緑矢印 振動方向:x軸 青矢印 振動方向: y軸 45゜の場合:波のベクトル表記が便利 波のベクトル表記が便利 一般化:各振動成分が非零の場合 φ :初期位相 ψ ωφ ψ xx(r, cost t)= −A x ( kr ) ψ(r, ,0,0t)=( ) ψ ωφ ψ.
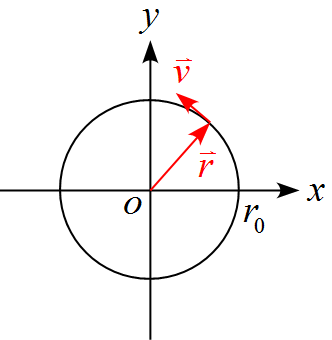
円 速度ベクトル. 3 ベクトル(vector)とスカラー(scalar) スカラー(scalar)・・・・大きさのみもつ量 (長さ,距離,速さ,仕事,エネルギー,時間,質量,電荷) ベクトル(vector)・・・大きさ,向き(方向)をもつ量 (変位,速度,加速度,力,運動量,力積) P点からQ点まで移動した場合. 1 速度と加速度(2)ー2,3 次元系ー 目次 §0 ベクトルとその性質と物理学で使われる理由 §1 .時間に依存するベクトルの微分係数(導関数). 円運動 等速円運動 物体が円周上を一定の速さで運動するとき、この運動を等速円運動といいます。単振動や波動を考えるときの大本となる運動です。 角速度 基準となる原点から運動している物体に引いたベクトルを動径ベクトルといいますが、等速円運動においては円の中心から物体に.
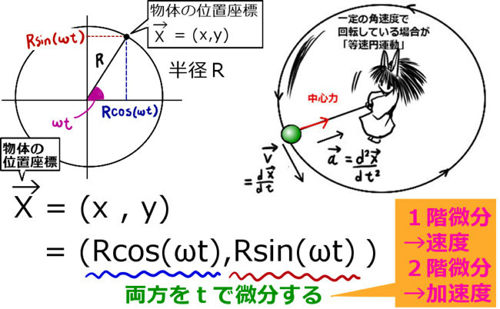
円運動(えんうんどう、英 circular motion )とは、物体の運動の向きとは垂直な方向に働く力によって引き起こされる運動である。 特に中心力(常に円軌道の中心を向き、大きさが距離のみに依存する力)が働くことにより引き起こされる。 とくに円運動は天体の運動の基本であり、ニコラウス. 円運動の運動方程式 — 角振動数一定の場合 — と同じく, 物体の運動が円軌道の場合の運動方程式について議論する ただし, 等速円運動に限らず成立するような運動方程式についての備忘録である このページでは, 本編の円運動の項目とは違い, 物体の運動軌道が円軌道という条件を初めから. 等速円運動の中心を原点 O ではなく任意の点 C (x C , y C) とすると,位置ベクトル r の各成分を表す式(1),式(2)は x (t) = R cos (ω t θ 0) x C (10) y (t) = R sin (ω t θ 0) y C (11) で置き換えられる(ここで,円周の半径を R とした). x C と y C は定数であるので,速度 v と加速度 a の式は.
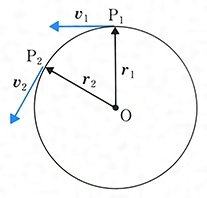
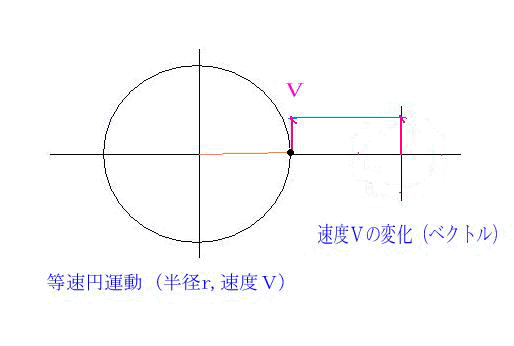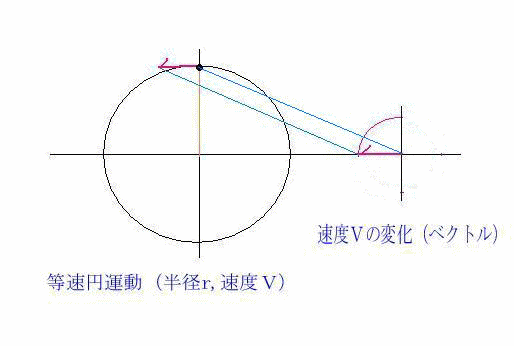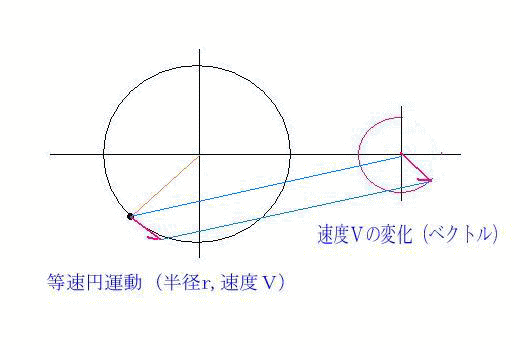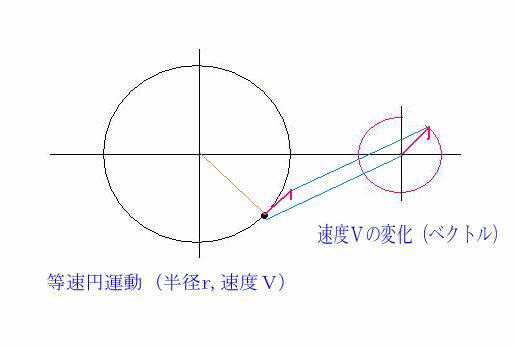
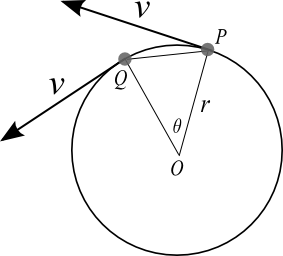
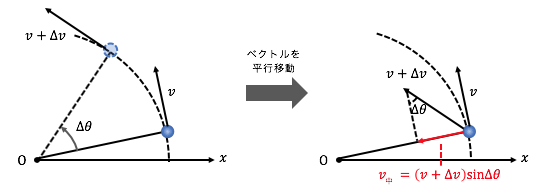
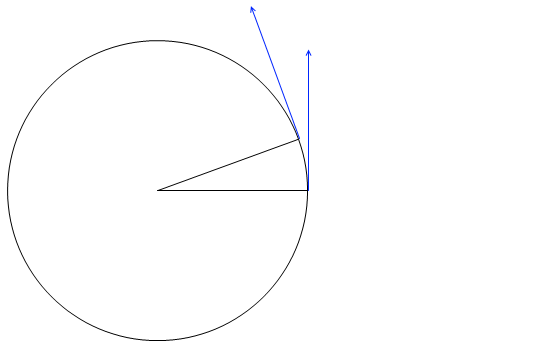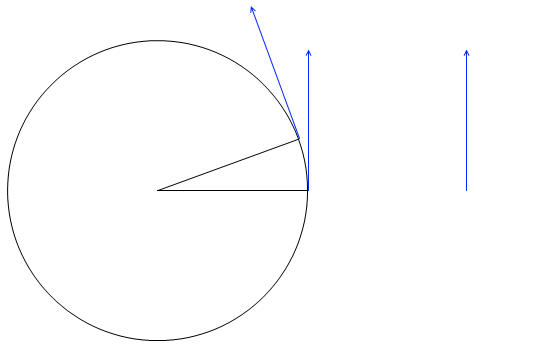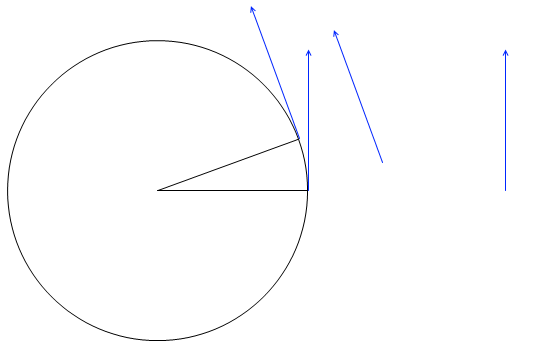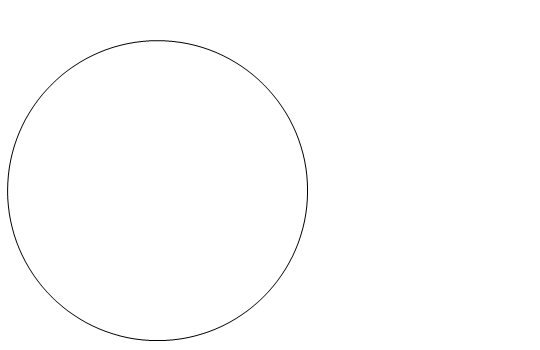
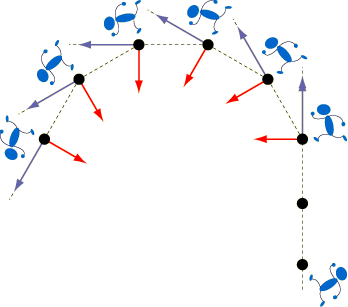
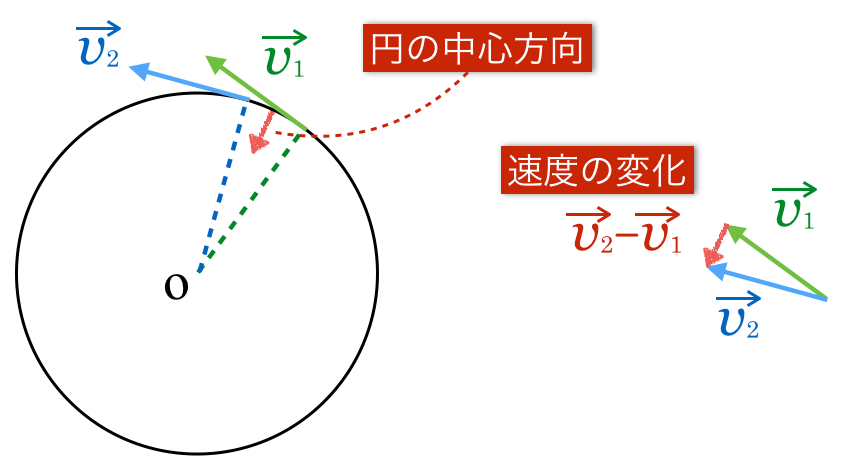
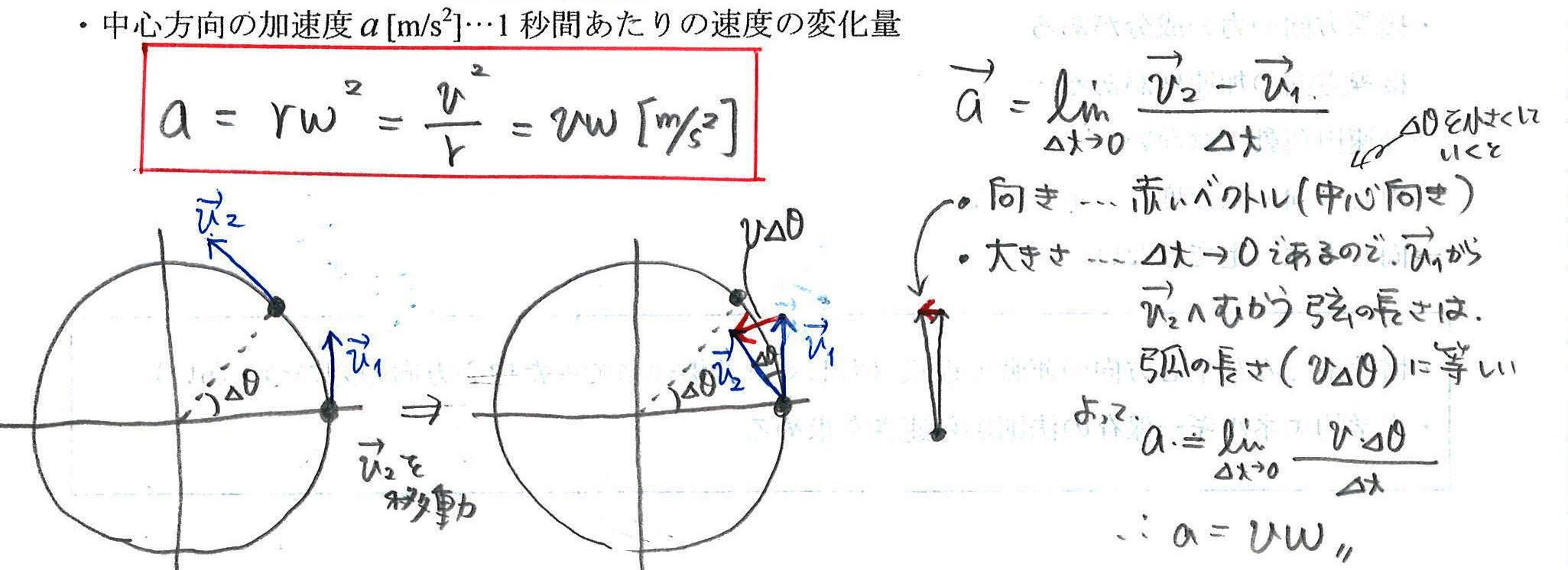
円運動をする物体の位置がpからqに変化した。 このとき、速度の大きさvは変わらないが、方向は変化している。 物体を中心として速度の変化を示した図が以下だ。 上の図からp点q点の速度ベクトルを平行移動して作成している。. R×m d2 r dt2 r× F (1014) となる。 右辺の!. である。このを角速度と言い、ωで表すこともある。 等速円運動の場合、角速度は一定なので dϕ dt =ω=ω 0, d2ϕ dt2 = dω dt =0 (922) である。この d2ϕ dt2 は角加速度という。 このことをふまえて、等速円運動の速度の極座標成分を求めると、 v r = dr dt =0, v ϕ =r dϕ.
速度と同様に、加速度はベクトル特性です。 ただし、その方向は速度ベクトルとは無関係です。 これはv¯の方向を変えることによって決定されます。 運動中に速度がそのベクトルを変えない場合、加速度aは速度と同じ線に沿って向けられる。. 多様体の基礎のキソ/接空間 3 この集合は実質的にRn と同じである.実際,C1 級曲線の速度ベクトルはいつもRn の 元であるし,任意のv 2 Rn にたいしx(t) = p tv (t2 R) とおけばp を時刻t= 0 に速 度v で通過するC1 級曲線(直線)になっている.(ただし,v = 0 の場合は定数写像.)そ. 速度の極座標成分を求める 今,r離れた質点が速度vで運動しているものとします.x軸方向をv x ,y軸方向をv y と成分を分解し,φが増える方向にv r ,v φ としてみて,これから,v r とv φ をv x ,v y を使って書き直すと, となるはず.一方, から,.
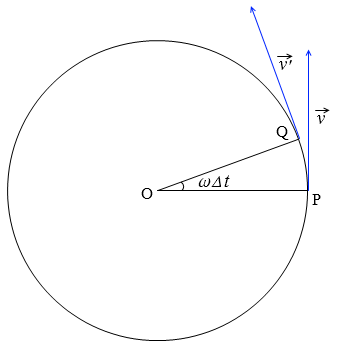
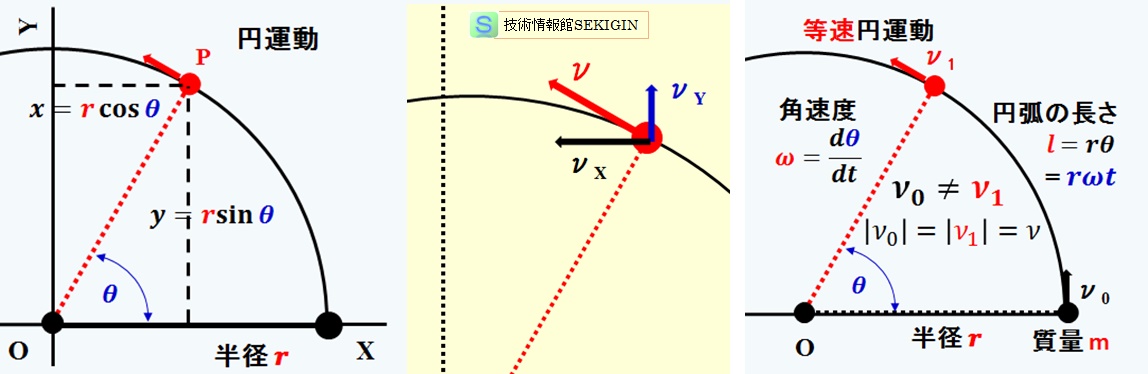
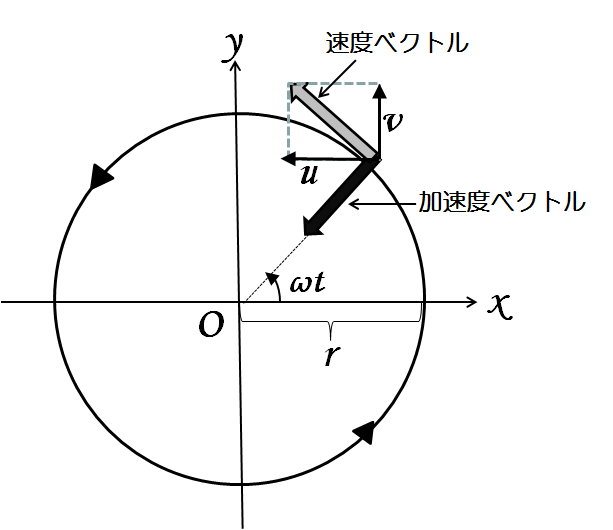
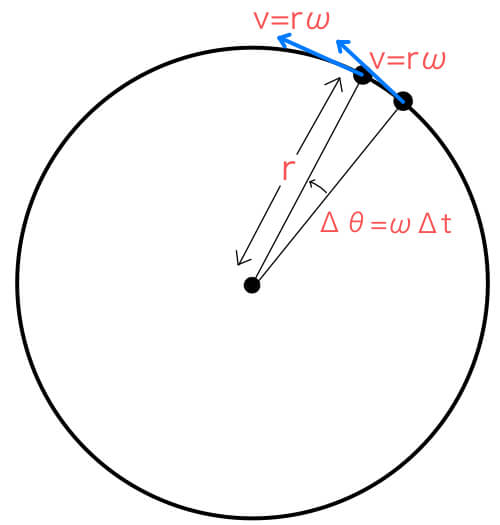
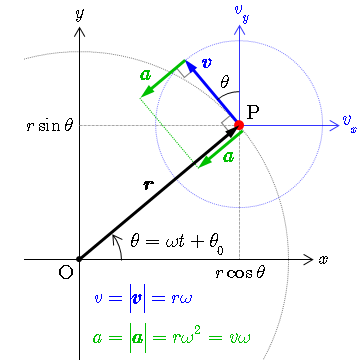
等速円運動は速さは一定だが,速度は一定ではない。 点Oを中心に,半径 r で一定の速さ v の等速円運動を考える。点P,P' それぞれの速さはv だが,つねに向きを変えている。 角速度ω(角度の時間変化の割合)を ()と定義する。単位はrad/s。. 02 速度ベクトルから式を導く 同じ三角関数の$\sin$と$\cos$を使いつつ、また違った方程式で等速円運動を表すことができます。運動の速度のベクトル$(x', y')$を、位置ベクトル(座標)に加えるのです。円運動の速度の$(x', y')$成分は、つぎの式で表されます。. よって速度ベクトルを引いていることに注意してください。つまり、x軸について見るとlinex0 – (thisx thisvelocityx)という計算を行っています。これはlinex0 - thisx thisvelocityxと同じ意味になります。 v1=円の速度ベクトル;.
等速円運動は速さは一定だが,速度は一定ではない。 点Oを中心に,半径 r で一定の速さ v の等速円運動を考える。点P,P' それぞれの速さはv だが,つねに向きを変えている。 角速度ω(角度の時間変化の割合)を ()と定義する。単位はrad/s。. 波のベクトル表記:波の振動方向を決める 緑矢印 振動方向:x軸 青矢印 振動方向: y軸 45゜の場合:波のベクトル表記が便利 波のベクトル表記が便利 一般化:各振動成分が非零の場合 φ :初期位相 ψ ωφ ψ xx(r, cost t)= −A x ( kr ) ψ(r, ,0,0t)=( ) ψ ωφ ψ. 今回からいよいよ動きのある表現(= アニメーション)について扱っていきます。アニメーションを実現するには、まず時間を扱う基本構造を知る必要があります。Processingでは、setup(), draw() という2つのブロックにわけて、初期化と更新を行うことでアニメーションを実現しています。まず始め.
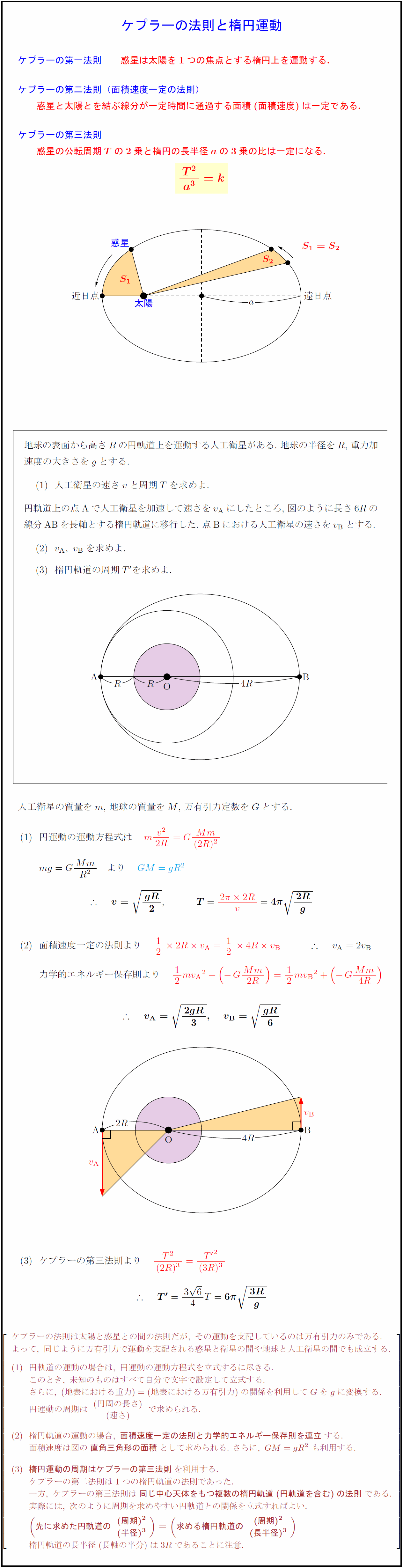
第7 章 円運動の動力学と惑星の運動 7–1 ケプラーの法則 1 惑星は太陽を一つの焦点とする楕円運動をする. 2 太陽と惑星を結ぶ線分が単位時間に描く面積は一定である(面積速度一定の法則).. 反射ベクトルは以下のようなベクトルです。 実は壁に平行なベクトルを求めることができたら、ほぼ反射ベクトルは求まっています。 以下の図を見てください。 進行ベクトルの終点に、仮に反射ベクトルの始点を置いています。. 左右方向速度 〓 上式により算出し,平 均速度,右 方向速度,左 方向速 度をもとめた。同様に前後方向についても行なった。 8)ベ ルクト a)位 置ベクトル 座標中心を中心として,各 ポイントの位置のベクトル を求め,8方 向区域に分けて,区 域毎の総和を求めた。.
等速円運動の定義 (パラメータ表示)・速度・周期・加速度・角速度等を解説しています。 等速円運動とは? ~速度・加速度など~ 理数アラカルト. 5.ベクトル解析1 ベクトル解析は、ベクトル値関数の微分積分学を展開する数学の分野の一部であるが、もともと は電磁気学など物理の法則などを表記するために生まれたものである。曲線を表現し解析するため に、また力学への応用にも役立つ。. また、この平均速度ベクトルの大きさを平均の速さと呼ぶ。 瞬間速度 平均速度を観測する際に、時間区分 t 2t 1 を十分小さくし 0 に近づけていくとき、各時点における速度とみなせるものが観測でき、これを時刻 t における瞬間速度 と呼ぶ。.
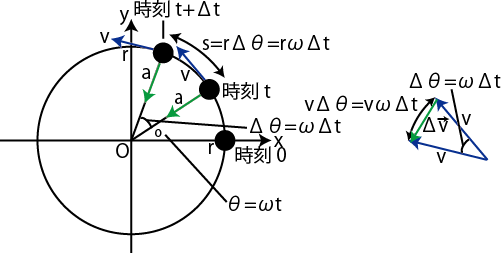
等速円運動では,加速度ベクトルと速度ベクトルは直交していることを 示せ v ·a = 0 223 速度ベクトルv と加速度ベクトルa 速度ベクトルはv = vet と書けることから、加速度ベクトルa は速度ベクト ルを時間微分することで a = d dt v = d dt (vet) = dv dt et v det dt (7. 円運動をする物体の位置がpからqに変化した。 このとき、速度の大きさvは変わらないが、方向は変化している。 物体を中心として速度の変化を示した図が以下だ。 上の図からp点q点の速度ベクトルを平行移動して作成している。. (2) 速度ベクトル$\vec{v}$と加速度ベクトル$\vec{a}$が直交していることを示せ。 (3) 加速度の大きさ$\vec{a}$を求めよ。 解答 直交を示す方法として、$\vec{v}\cdot\vec{r}=0$を示す方法を用いる。 $\vec{r}$と$\vec{v}$のそれぞれをそれ自身と内積を取ると 等速円運動より.
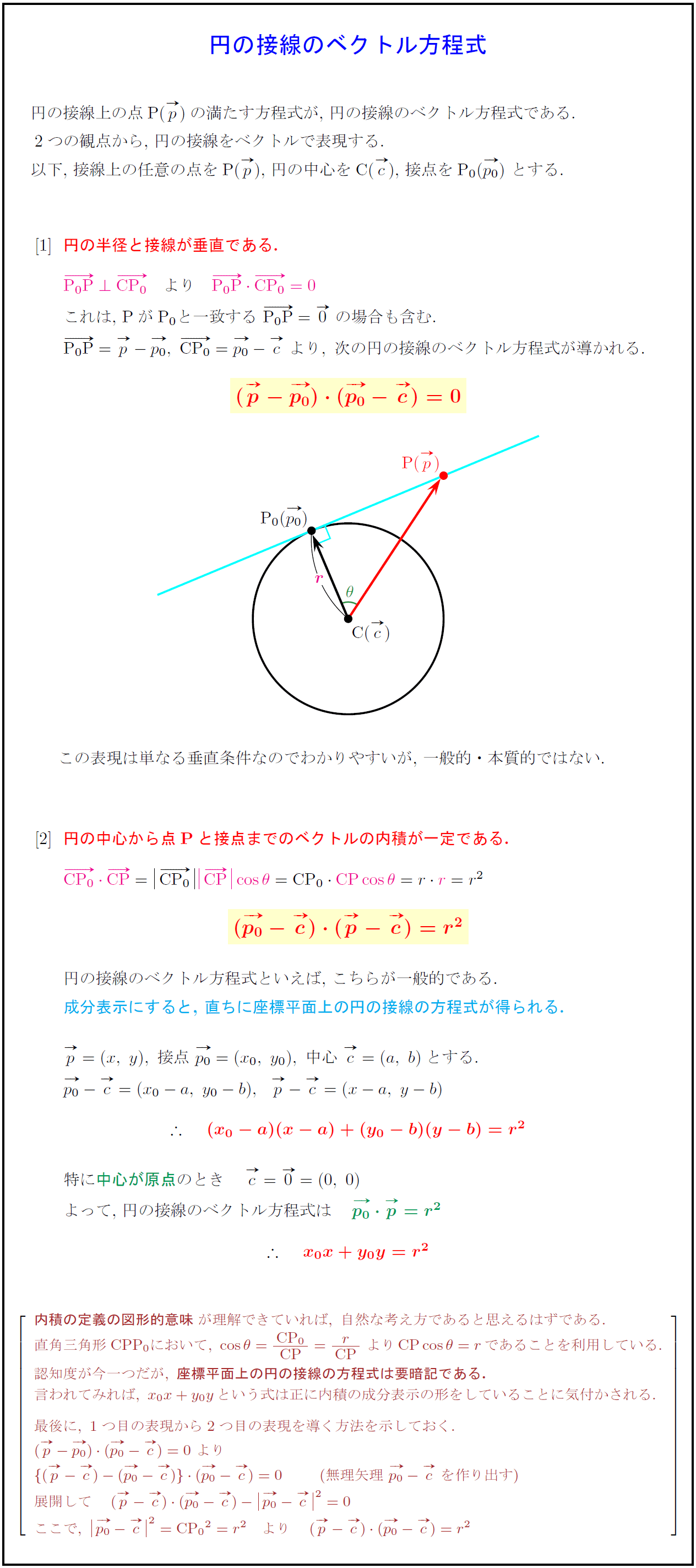
円のベクトル方程式 直線のベクトル方程式は、基本直線のベクトル方程式や基本2点を通る直線のベクトル方程式で見ました。 円に対しても、同じようにベクトルで考えてみましょう。 円というのは、中心からの距離が一定の点が集まったものですね。. 66 第6 章 中心力のもとでの運動 面積速度 時刻t に位置r にあった質点が,微小 時間後のtΔt にrΔr に移動したとする。 微小 時間Δt のあいだに位置ベクトルが掃いた面積ΔS は,r とΔr を2辺とする三角形の面積で近似でき る(図63)。 Δr の大きさをΔr と表し,r とΔr とのなす角を. 一定、の時、速度ベクトルと加速度ベクトルは直交する。例 等速 円運動 一定 一定 動、というのではない 、注意 速さ 一定 等速円運 であるから、 一定、でも とは限ら ない。 また、単位ベクトルを微分すると、そのベクトルはもとのベクトルに直交する。!.
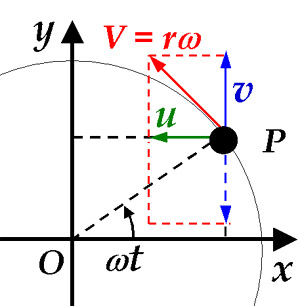
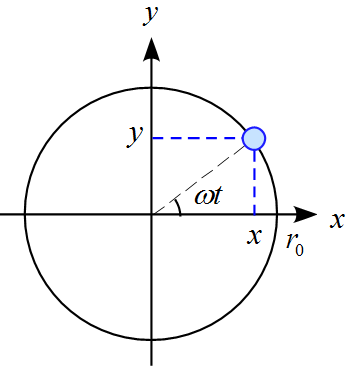
解説 円の中心を原点とするxy平面上で物体が等速円運動しているとします。 動径ベクトルがx軸から反時計回りに角q のところにあるとします。 時刻 に動径ベクトルがx軸となす角をd として、 です。 物体の座標を として、 , ・・・① 物体の速度を として、 , ・・・②. 円運動の速度・加速度 円運動のイメージがついたところで、 具体的な取り扱い方を考えていきます。 既に勉強した通り、 何か運動を考えたかったら、 運動方程式を考えるのが普通です。 しかし今回は、 今まで通り考えることはできません。. R× Fのことを力のモーメントまたはトルクと呼ばれるベクトル量 Nで物体を 回転させようとする力の効果を表す。.
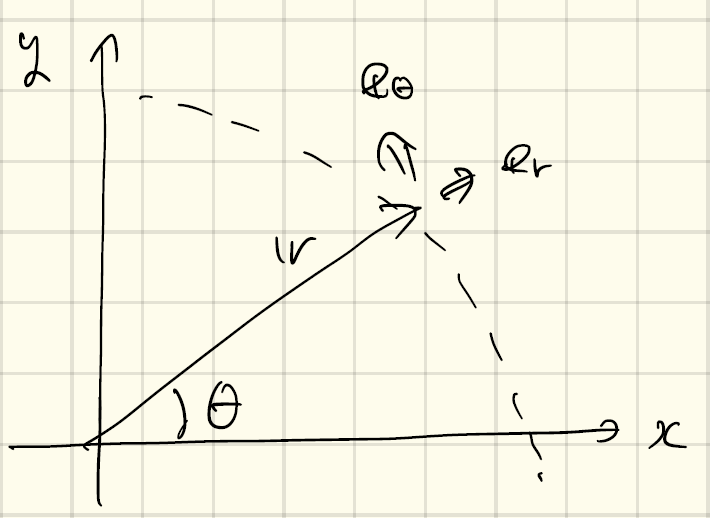
52 第5章 極座標による運動の記述 任意のベクトルの極座標表現 任意のベクトルA は極座標系の3つの単位ベクトルの 線形結合で表すことができる A = A r e r A θ e θ A ϕ e ϕ (55) ここで,各成分はベクトルA と極座標系の単位ベクトルとのスカラー積 A r = e r · A,A θ = e θ · A,A ϕ = e ϕ ·A (56).
円運動の加速度
等速円運動の位置 速度 加速度
向心力 わかりやすい高校物理の部屋
高校物理 ケプラーの法則と楕円運動 受験の月

円運動の速度と加速度 御光堂世界 Pulinの日記
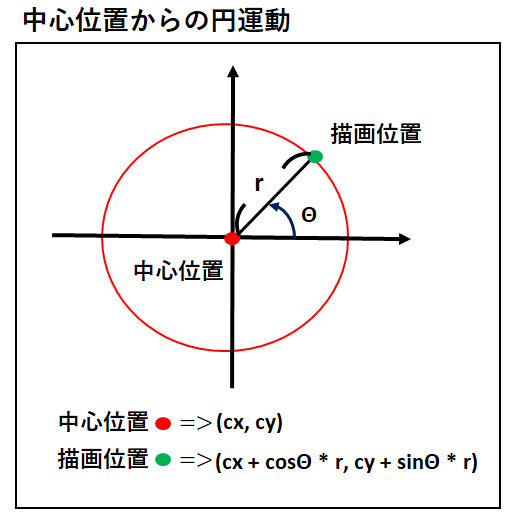
ゲーム 円運動
等速円運動

円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ
角速度wで半径rの円周上を等速円運動する点pについて 位置ベクトルr 速度v Yahoo 知恵袋
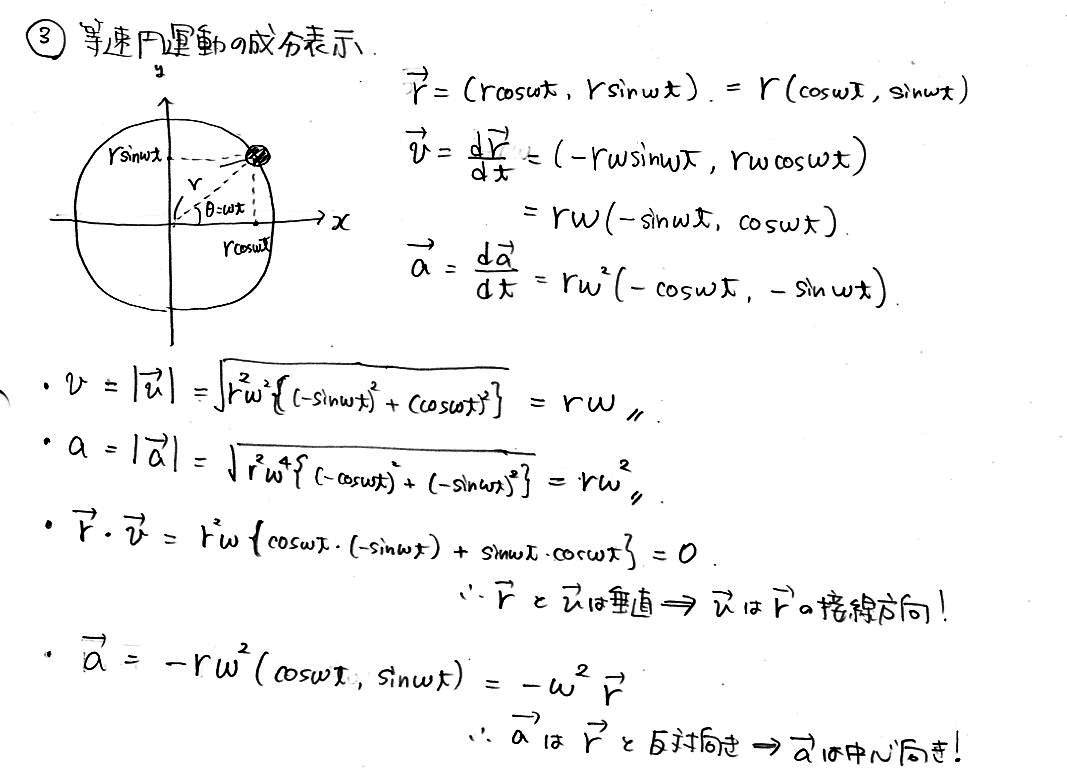
Adoko 力学 円運動
物理 古典力学の基礎 円運動 剛体の運動 技術情報館 Sekigin 円運動に関連し 等速円運動 向心力 周期 角振動数 剛体の運動 慣性モーメント トルク 回転運動 に項目を分けて紹介する

円運動 高校物理の備忘録
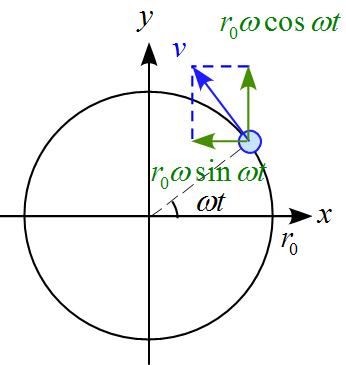
未整理 011
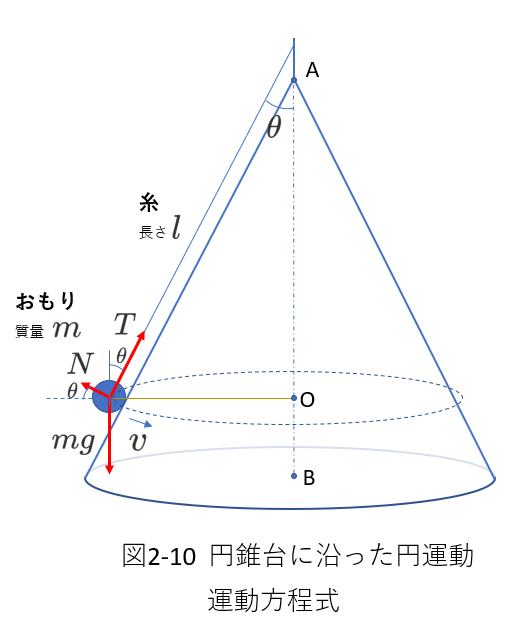
円運動

高校物理 向心力と等速円運動の基本 受験の月
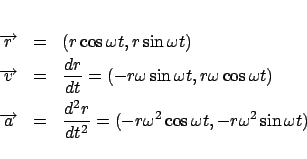
等速円運動の速度と加速度
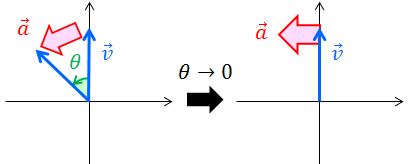
等速円運動 Nagatabi P ページ
Q Tbn And9gctlxzepdia4cugmtewkz0tljpx7pojdcqcpd6ckqmcdwod7zegg Usqp Cau

大学受験 円運動の公式証明 あらんのブログ
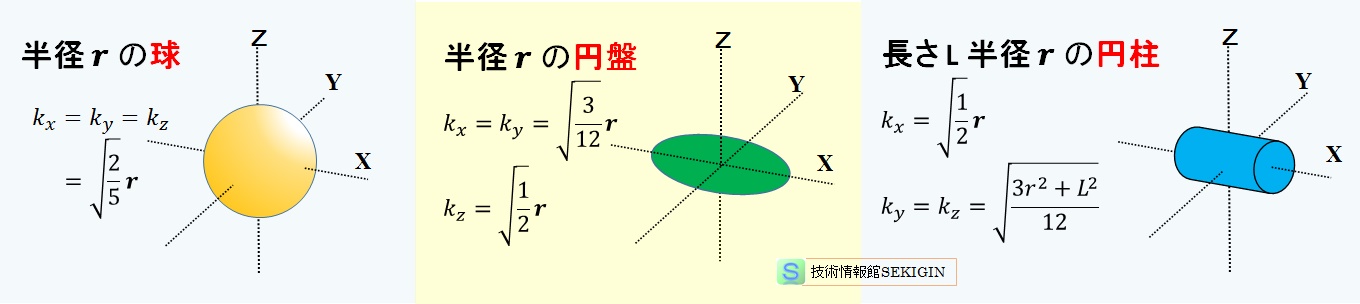
物理 古典力学の基礎 円運動 剛体の運動 技術情報館 Sekigin 円運動に関連し 等速円運動 向心力 周期 角振動数 剛体の運動 慣性モーメント トルク 回転運動 に項目を分けて紹介する

高校物理 入試に頻出 等速円運動 力学 お茶処やまと屋
円運動の加速度 物理学解体新書

等速円運動を三角関数により位置と速度のふたつの方程式で表す Qiita

等速円運動の位置ベクトル 速度ベクトル 加速度ベクトル Youtube
図解でわかる 円運動を東大院生が解説 速度 加速度の求め方 受験メモ

Adoko 力学 円運動24年度
地学自主ゼミ 3 遠心力のはなし Fidelio

円運動の運動方程式 高校物理の備忘録

高校物理 等速円運動の速度と加速度 映像授業のtry It トライイット
高校数学b 円の接線のベクトル方程式2パターン 受験の月
回転している円盤上の点の速度ベクトル Takaのblog

円運動の運動方程式 高校物理の備忘録
等速円運動の 速度ベクトルと加速度ベクトルが反平行になることを示すには Yahoo 知恵袋
物理位置ベクトルと速度ベクトルが垂直であることを示せ 問題 質 Yahoo 知恵袋
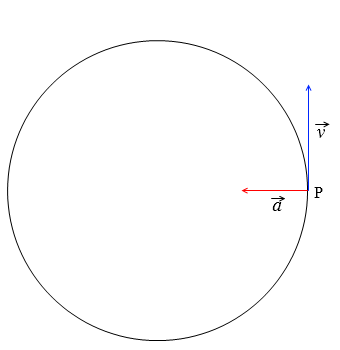
向心力 わかりやすい高校物理の部屋
円運動物体の求心加速度 Techistory
Q Tbn And9gctlxzepdia4cugmtewkz0tljpx7pojdcqcpd6ckqmcdwod7zegg Usqp Cau
向心力 わかりやすい高校物理の部屋

角速度 Wikipedia
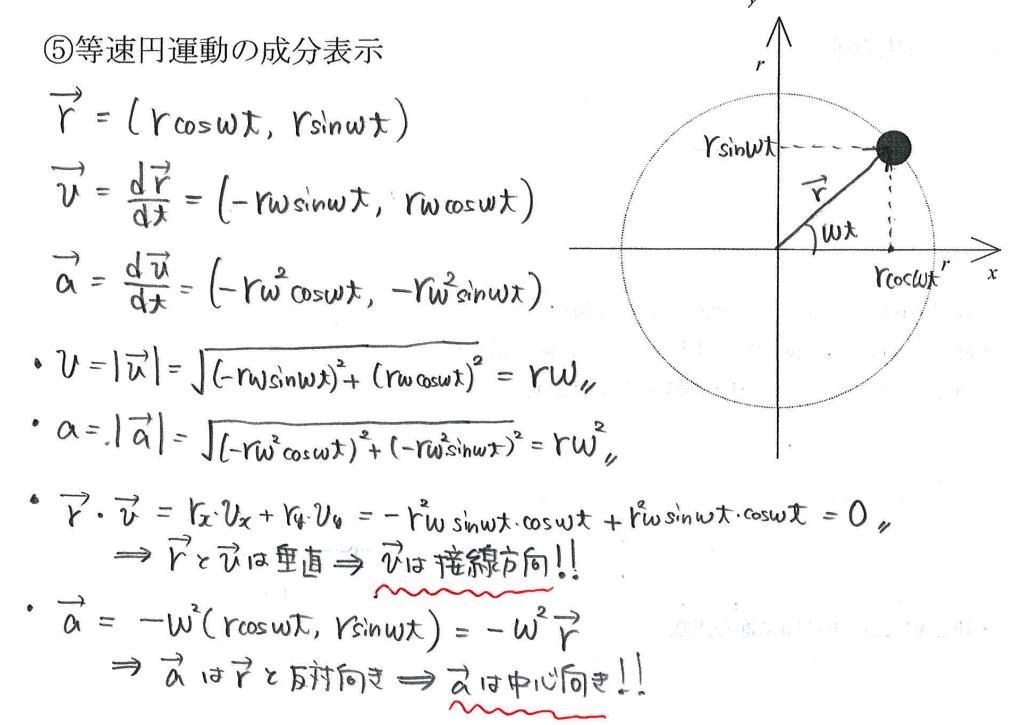
Adoko 力学 円運動24年度
わかりやすい 円運動の基礎 遠心力を含む かきのたねブログ
J Simplicity 例3 等速円運動
等速円運動 物理のかぎしっぽ
円運動

遠心力と求心力 物理の力学で出てくる等速円運動 等速直線運動 加速度運動の次にでてくる項目だと思いますが 遠心力や求心力の公式で半径は分子 分母 どっちだっけと迷ったことはありませんか 微積分の確立に物理学者でもあるニュートンが関わっ

角速度の公式と求め方 見やすいイラストで一発理解 計算問題付き 高校生向け受験応援メディア 受験のミカタ

角速度の公式と求め方 見やすいイラストで一発理解 計算問題付き 高校生向け受験応援メディア 受験のミカタ
力学 2 運動の記述と数学の基礎 Yukishiomi Note

円運動 高校物理の備忘録
水車の回転速度で考えるベクトルの回転 rot その2 Jo3krpの独り言

速度ベクトルと加速度ベクトル 11 9 11章 ベクトル 数学大百科事典 Youtube
等速円運動 物理のかぎしっぽ

24時間ではしりぬける物理 補講その13 等速円運動の速度 加速度とベクトルの微分 Youtube
古典力学とベクトルの微積分 理数系無料オンライン学習 Kori
等速円運動 位置 速度 加速度

高校物理 等速円運動の加速度 映像授業のtry It トライイット
円運動の中心力

中学生にもわかるアインシュタインの数式本文305
Q Tbn And9gcseqp2rvo1you1ss7vi336rszpzpsz2zduyhyjvalzduwivau3 Usqp Cau

2次元極座標系の運動方程式 高校物理の備忘録

円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ

高校物理 等速円運動の加速度 映像授業のtry It トライイット

回転している円盤上の点の速度ベクトル Takaのblog
センター17物理追試第1問 問1 等速円運動の加速度と力の向き 理科が好き Com
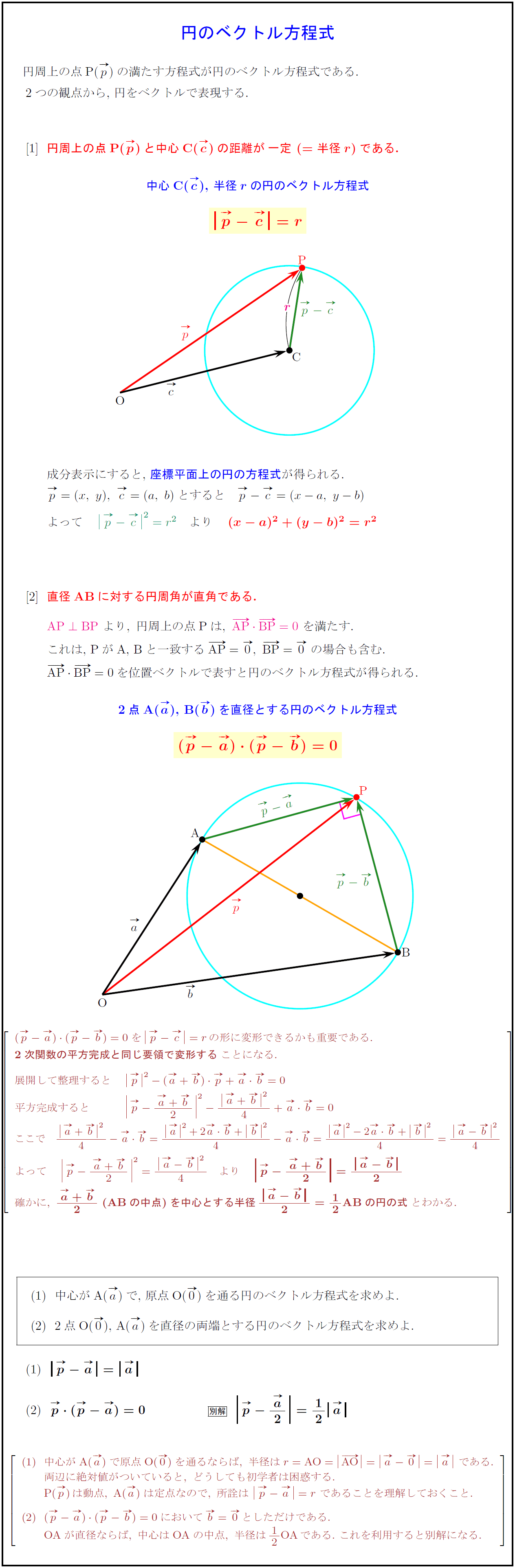
高校数学b 円のベクトル方程式2パターン 受験の月
Uor642eo9ah87f Com E5 90 91 E5 Bf E5 8a A0 E9 80 9f E5 Ba A6 81 A3 81 A6 E4 95 Ef 9f Ef 81 E8 92 E9 80 9f E5 Ba A6 81 81 E5 86 86 E9 81 8b E5 8b 95 81 Ae E5 85 Ac E5 8f 92

高校物理 円運動の速度の方向と大きさ 映像授業のtry It トライイット

2 10 極座標を使ったベクトルの微分
Adoko 力学 円運動24年度

円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ
未整理 011
等速円運動でわからないところがあります 速さv Rwsinwt Rwco Yahoo 知恵袋
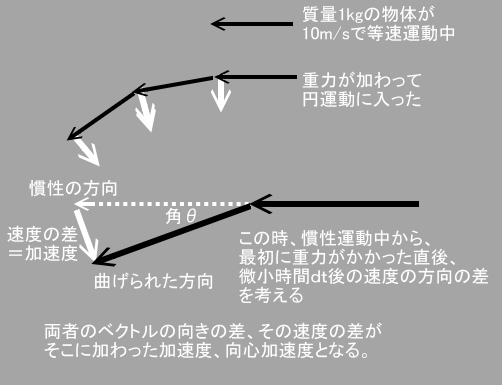
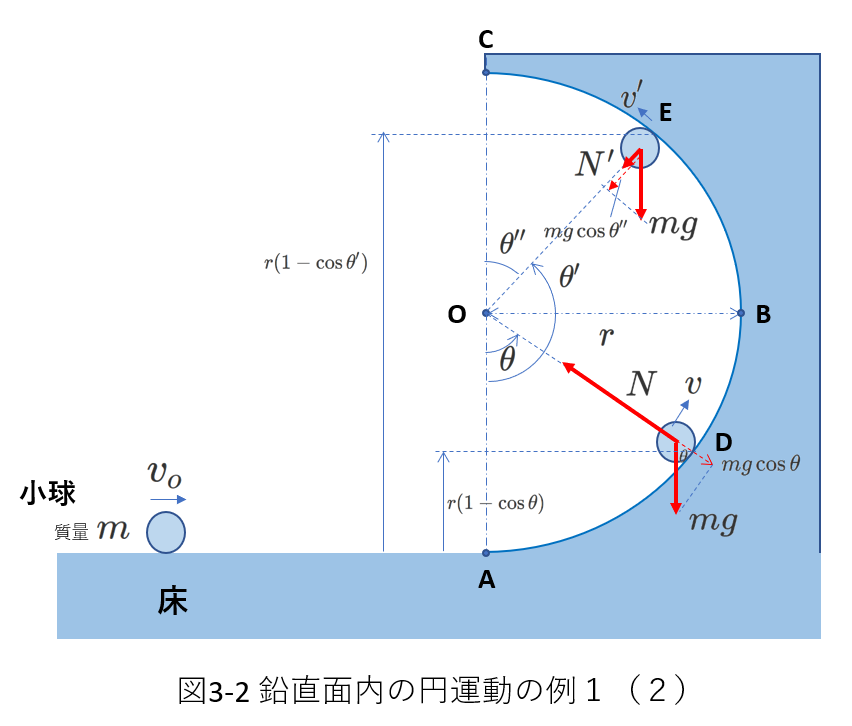
円運動の加速度 ここで円運動で常に中心方向にかかり続ける力 すなわち向心力の量を求めて見ましょう これを求めるのは速度もベクトルなのだ というのとそこから加速度を読み取れるのだ という点のとても分かりやすい例の上 向心加速度も重要な
物理の等速円運動について質問します 加速度aは位置ベクトルr Yahoo 知恵袋

物理教室

高校物理 入試に頻出 等速円運動 力学 お茶処やまと屋
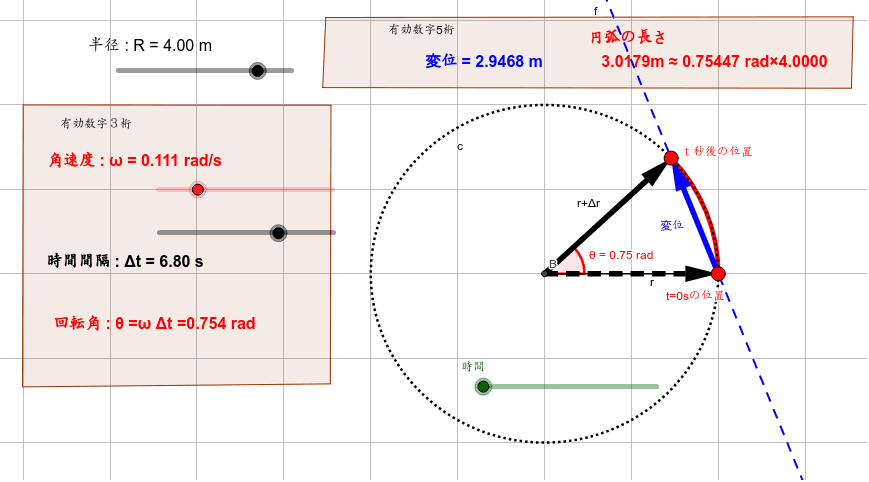
円運動 変位と速度 Geogebra
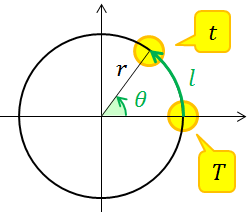
等速円運動 Nagatabi P ページ

円運動の運動方程式 高校物理の備忘録
Uor642eo9ah87f Com E5 90 91 E5 Bf E5 8a A0 E9 80 9f E5 Ba A6 81 A3 81 A6 E4 95 Ef 9f Ef 81 E8 92 E9 80 9f E5 Ba A6 81 81 E5 86 86 E9 81 8b E5 8b 95 81 Ae E5 85 Ac E5 8f 92
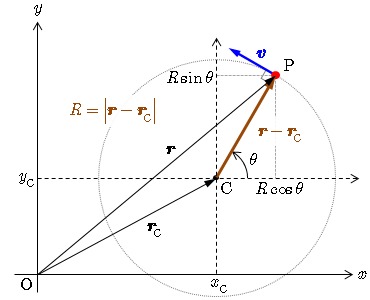
等速円運動 位置 速度 加速度

物理 円運動

適当な調査 遠心力の理解
加速度ベクトルと速度ベクトルの内積は等速円運動においては常に0ですか Yahoo 知恵袋

角速度 Wikiwand

適当な調査 4月 15
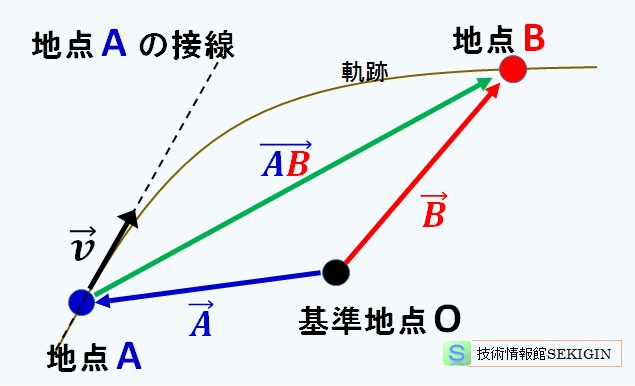
物理 力と運動 速度 加速度 技術情報館 Sekigin ここでは 運動の表し方に関連し 速さと速度 変位と速度 加速度 に項目を分けて紹介する
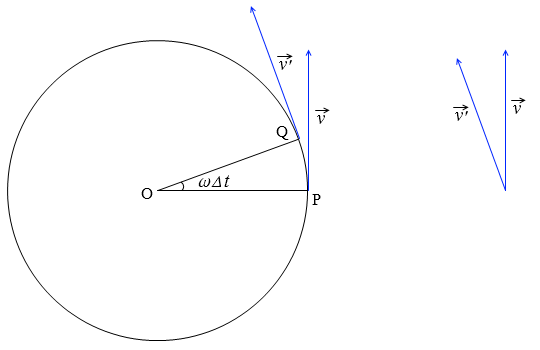
向心力 わかりやすい高校物理の部屋
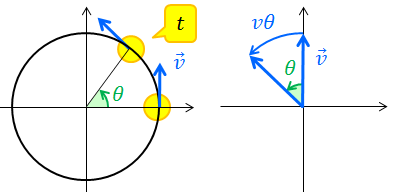
等速円運動 Nagatabi P ページ
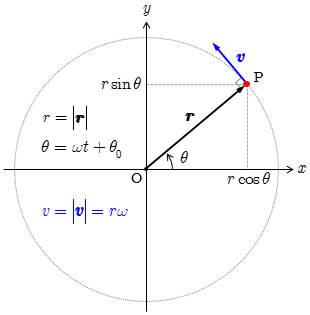
等速円運動
角速度が一定とは限らない一般の円運動において 位置ベクトルrベクトル 速度ベク Yahoo 知恵袋
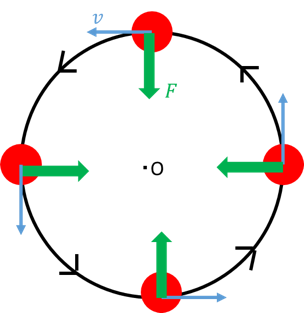
Hiro Academia 偏差値30からの早稲田慶應専門個別指導塾といえば

平面上の速度 加速度 高校数学に関する質問 勉強質問サイト

速度レベルインジケータ低く高いスケール黒と赤のバロメーターレベル最小および最大レベル円の中の評価図ダウンロードとアップロード速度ベクトルeps 10 いっぱいになるのベクターアート素材や画像を多数ご用意 Istock

高校物理 等速円運動の加速度 映像授業のtry It トライイット

等速円運動 Koko物理 高校物理

等速円運動 富岡市の総合学習塾 トータルアカデミー
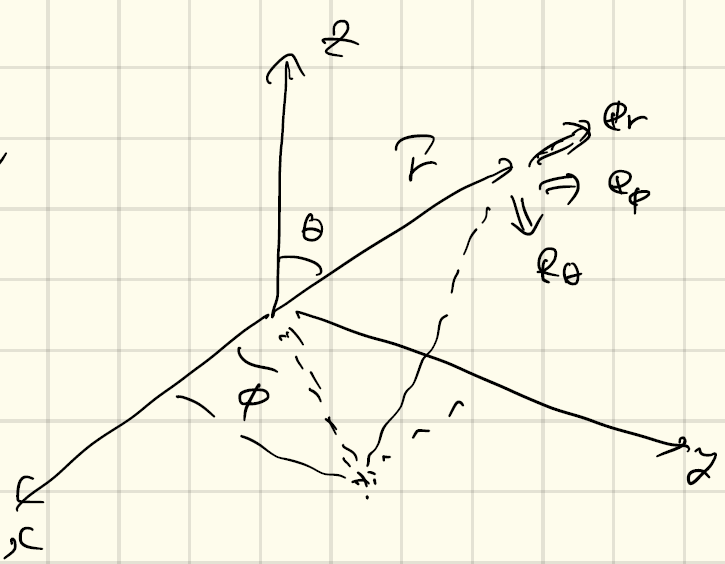
力学 2 運動の記述と数学の基礎 Yukishiomi Note



